Computer Vision Project help
- Dec 15, 2021
- 3 min read
Updated: Dec 28, 2021
Problem 1
We have discussed the 2D planar perspective transformation, also known as 2D homography, which maps a point (x, y) to a new location (x′, y′) in the plane. This transformation can be represented using the following equation.

When using homogeneous coordinate representation as shown here, recall that s is simply a scalar term that is to be eliminated when solving for (x′, y′). As discussed in the textbook near equations (2.20)-(2.21), there are only 8 degrees of freedom in this equation. For this reason, many formulations set 𝑎𝑎9 to 1. It may help you when working on coding problems later if you do not constrain 𝑎𝑎9 to be 1.
a) Consider the case that you are given 𝑛𝑛 corresponding pairs of points, where 𝑛𝑛 ≥ 4, and you want to use those points to determine the parameters 𝑎𝑎1 through 𝑎𝑎9. For example, assume that the following correspondences are known:

Show how to derive one matrix equation that represents the relationship between these all of these scalar values (not including s). The form of the equation should be 𝑸𝑸 𝒂𝒂 = 𝟎𝟎, where 𝒂𝒂 is a 9x1 vector that contains the individual homography parameters only; 𝑸𝑸 is a matrix of size 2nx9 that you specify containing known values; and 0 represents the 2nx1 vector containing only values of 0. For this part of the problem, you do not need to solve for the parameter vector 𝒂𝒂. Hint: you may find some inspiration in the derivation near the end of packet 5, although those lecture slides are discussing a problem that is different from 2D homography
b) Continuing from part (a), a least-squares solution to parameter vector 𝒂𝒂 is the eigenvector associated with the smallest eigenvalue of the matrix 𝑸𝑸T𝑸𝑸. Use this approach to find numerical solutions for homography parameters 𝑎𝑎1 through 𝑎𝑎9 for the following point correspondences:

To help with the grading, please normalize your numerical solution by dividing all parameters 𝑎𝑎1 through 𝑎𝑎9 by the value of 𝑎𝑎9.
You may use any matrix solver to find the numerical values. For example, the NumPy functions np.linalg.eig() or np.linalg.eigh() might be used. If you use a matrix solver, cut and paste your code as part of your solution.
Problem 2
Consider the simple stereo imaging geometry that was introduced in class, as shown below. Both optical axes are parallel, and both cameras have the same focal length. In this view from above, the overall coordinate reference frame (x, y, z) is centered at the left camera.

Assume that all distances are given in units of meters. Let f = 0.035 and B = 0.15. Suppose that you are given the following corresponding pair of points from the two images:
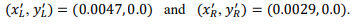
Solve for the 3D point (x, y, z) that is associated with these two image points.
Problem 3
Consider again the stereo imaging geometry from the previous problem. Now assume that you have implemented a stereo matching procedure that has produced an incorrect horizontal disparity value, 𝑑𝑑 + ∆𝑑𝑑, where 𝑑𝑑 is the correct disparity and ∆𝑑𝑑 is an unknown error. When your system solves for the corresponding 3D location, the computed depth will be 𝑧𝑧 + ∆𝑧𝑧, where z is the correct value and ∆𝑧𝑧 is the error that results from ∆𝑑𝑑. Try to find an expression for ∆𝑧𝑧 that is a function of z, d, and ∆𝑑𝑑 only. Collect terms and give a simplifed expression. (Do not plug in numerical values for B, f, z, d, etc.)
Problem 4
You have been given some image files and a Jupyter notebook file named Homework3_USERNAME.ipynb. Replace “USERNAME” with your Virginia Tech Username. Then upload all of these files to Google Drive. Open the ipynb file in Google Colab. Follow the instructions that you will find inside the notebook file.
Problem 5
Near the end of your Jupyter notebook file for the previous problem, append new code blocks and text blocks in which you make comparisons between SIFT-based and ORB-based keypoints. Do not change your answers for Problem 4, but instead add new blocks at the end of the notebook file in which you write code that detects both types of keypoints. You may use images that have been provided to you, or you may upload images of your own. Add text block(s) in which you discuss the relative merits of these two types of keypoints. Try to find cases in which SIFT performs better than ORB, and vice versa. Clearly indicate those cases to the grader. You may discuss differences the accuracy of matches that are reported, differences in computation time, or other differences that you find to be interesting.
You do not need to provide a lengthy report for this problem. Roughly 1 or 2 pages of discussion might be expected, in addition to interesting displays of images/figures that illustrate your findings.



Comments